The family of burr or notched-stick puzzles is a large and prolific one, with offspring numbering in the hundreds or even thousands depending upon how one counts them, and with more being born all the time. This book is not intended to be a compendium of puzzle inventions, past and present. One yardstick for inclusion is the extent to which the underlying idea behind the puzzle is logical and mathematical rather than simply mechanical. Symmetry is an important consideration. In this chapter we will conclude the discussion of square-stick burrs by considering only those having certain kinds of symmetry. This is an appropriate point at which to discuss symmetry.
The term isometric symmetry was introduced without explaining what it meant. A three-dimensional object is said to have isometric symmetry if it has identical non-coplanar axes of symmetry. In other words, it exists in a sort of geometrical vertigo, with no identifiable upright orientation, no top or bottom, front or back, left or right, all being the same. All of the Platonic solids have this property, including their various truncated and stellated variants. Rectangular solids (except the cube) and pyramids (except the tetrahedron) do not have it. The three-dimensional object in question can be anything from a polyhedral solid to a cluster of solids, a nesting of sticks, or whatever.
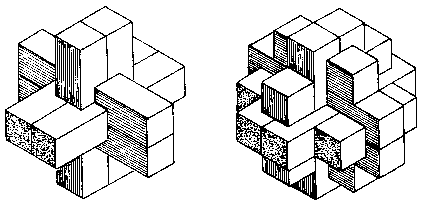
There is another sort of symmetry that most of the burr puzzles in this book have, sometimes referred to as homogeneity or congruence. It is illustrated by the two drawings in Fig. 72. On the left is the standard six-piece burr. The 12-piece burr on the right is representative of a popular family of puzzles, sometimes called pagodas. which lack homogeneity because not only are the sticks of various lengths but also their relative positions are distinguishable.
Fig. 72
The term homogeneous isometric symmetry is so awkward that it will not be used throughout this book, but rather will be implied. Most well-conceived burr puzzles have it, and the lacking of it must be considered an aesthetic blemish. Like so many aesthetic considerations, this one too is rooted firmly in practicality. Most interlocking puzzles have a key piece or sliding axis that constitutes the first step of disassembly. In a symmetrical burr, all pieces have equal standing and are indistinguishable from one another when assembled, thus coyly hiding their identity beneath a geometrical masquerade.
A distinction is made between apparent symmetry and total symmetry. When a puzzle has apparent symmetry, as do practically all well-designed geometrical puzzles, the assembled external shape is symmetrical but not necessarily the insides. When a puzzle has total symmetry, all of the internal surfaces of dissection are symmetrical as well. Such puzzles necessarily have all pieces identical, limiting their possibilities for combinatorial problems, but there are some intriguing exceptions involving color symmetry.
For both practical and aesthetic reasons, as already discussed, anyone who tinkers with geometrical puzzles usually takes for granted the concept of symmetrical external form and internal dissymmetries without giving it much thought. It is interesting to note that all higher animals also have this property, although the exact reasons for it are not at all obvious. If one's body and brain were entirely bilaterally symmetrical, could one tell the difference between left and right, throw a ball, or use a typewriter? Could one even think, in the usual sense of the term?
Symmetrical rectilinear burrs can be made of 3, 6, 12, or 24 sticks - no other sizes are possible. The basic six-piece burr was discussed in the previous chapter. The most obvious form for the 12-piece burr is that shown in Fig. 73 on the left. Notice that the axes of the intersecting sticks are not offset as in the six-piece burr, but instead intersect with each other. In order to understand what problem this creates, consider the simple three-piece burr shown in Fig. 73 on the right.
Fig. 73
A little reflection should convince the reader that with any sort of conventional rectilinear notching, the three-piece burr is impossible to assemble, or even more obvious, impossible to disassemble. When you see a three-piece burr of this type, you can be sure that either one of the notches has been rounded so that a piece rotates, or else the sticks have diagonal or otherwise unconventional notches. The same applies to the 12-piece version.
One way of overcoming the problem just explained is to space the sticks apart in the 12-piece burr, as shown in Fig. 74 on the left. Symmetry is maintained. The possibilities for notching combinations are virtually limitless. There is well-known variation of this with the sticks spaced farther apart so that it resembles a cage (Fig. 74 in the center). Sometimes a ball is placed inside. There is yet another variation, but non-homogeneous, with three more pairs of sticks added to fill the center spaces, even more complicated to design, to solve, or even to explain (Fig. 74 on the right).
Fig. 74
There is one other symmetrical 12-piece burr that is a classic and quite unlike any of the others mentioned thus far. It is shown assembled in Fig. 75a, together with one of its 12 pieces, all of which are identical. US Patent No. 430,502 was granted to William Altekruse in 1890 for this puzzle. The puzzle has been popular for a long time and manufactured in many different forms with many different names (except Altekruse). The Altekruse family is of Austrian-German origin. Curiously, the name means "old cross" in German, which has led some authors to incorrectly assume that it was a pseudonym. A William Altekruse who is presumed to be the grantee of the patent came to America as a young man in 1844 with his three brothers to escape being drafted into the German army. Could he have brought at least the germ of the idea with him? Whatever the case, it is a most interesting burr. By the way, note that if one insists on being precise, it is not quite symmetrical visually because the asymmetrical notch arrangements reveal themselves.
Fig. 75a
The Altekruse Puzzle, sometimes known as the 12-piece burr, has an unusual mechanical action in the first step of disassembly by which two halves move in opposition to each other. This may come as quite a surprise to those accustomed to the more familiar burr types with a key piece or pieces. Depending upon how it is assembled, this action can take place along one, two, or all three axes independently but not simultaneously. If two extra pieces are available, there is a surprising 14-piece solution shown in Fig. 75b. It was made from mahogany by Tom Lensch.
Fig. 75b
The interesting variations of this puzzle are quite numerous, and probably others await discovery. In the standard Altekruse Puzzle, each piece has three notches, with the two end notches facing in the same direction. There is a variation in which some pieces have notches facing in opposite directions, and such pieces can be either one of a reflexive pair, as illustrated in Fig. 76. Which combinations using such pieces are possible?
Fig. 76
The repetitive structure of Altekruse pieces can be extended indefinitely to create larger puzzles. Before considering these, note the diminutive version shown in Fig. 77 that uses six pieces of two notches each - three right-handed pieces and three left-handed. Try to solve this puzzle visually, and then discover an interesting variation that does not use equal numbers of right-handed and left-handed pieces (and do not forget that it must be assemblable).
Fig. 77
There is a version that uses 24 sticks, four notches in each, 12 right-handed and 12 left-handed (Fig. 78 on the left). There is a version that uses 36 or 38 identical sticks of five notches each (Fig. 78 on the right), and so on ad infinitum. There are rectangular versions in even greater number. Note that none of these larger versions is homogeneous. Once the basic principle is understood, these larger versions are not very difficult to assemble except that some trial and error may be required to figure out the correct order of assembly. They also require more dexterity of the others, and it helps if the pieces are accurately made.
Fig. 78
Another interesting variation of the Altekruse Puzzle uses pins and holes in place of notches. In its simplest version each piece has one pin and one hole, with six right-handed pieces and six left-handed pieces. An unusual feature of this version is that, with a large supply of pieces to work with, they can be connected end-to-end to make longer sticks and larger, more complex assemblies without limit. To make things more interesting, there need not be equal numbers of the two types of pieces, and there may also be pieces with pins facing in opposite directions. For even more entertainment, add pins or holes in the centers of the pieces (Fig. 79). Just figuring out all the possible pieces is quite a task, and analyzing all of the 12-piece assemblies should keep someone occupied for a long time.
Fig. 79
Like the design described above, this one also uses pins and holes. The basic puzzle consists of six 1 x 1 x 3 bars and six dowels of length 3. Each bar has three holes slightly larger than the dowels. The puzzle pieces are fabricated as shown in Fig. 80, using brads to hold the dowels in place. One version of the puzzle uses one pin, one bar, two crosses, and three elbows. This puzzle can be assembled one way only but is quite easy.

Fig. 80
By having larger sets of pieces and including one more type of piece twice as long, many larger and more complicated figures can be constructed. Two examples of which are shown in Fig. 81.

Fig. 81
The Pin-Hole Puzzle has an interesting variation. Eight cubic blocks are added to the corners of the Pin-Hole Puzzle, making the assembled shape cubic (Fig. 82a).
Fig. 82a
Each cubic block might be attached to any one of the three bars against which it rests. Thus, the puzzle designer faces a choice of 38 or 6,561 different ways of attaching the blocks. Another way of looking at the problem is to consider all the different types of pieces that could result. When one considers all the ways that one or two blocks can be added to the three basic pieces (bar, cross, elbow), there are 18 possible augmented pieces. Six of these are less desirable because they have an axis of symmetry, leaving the 12 pieces shown in Fig. 82b. Problem: from this set of 12 pieces, find a subset of six pieces that assembles one way only. The author has tinkered with this problem off and on for years without success. For some reason not understood, the solutions always seem to occur in pairs or more. To simplify the problem somewhat, note that piece 1 must always be used, plus three more pieces with single blocks and two with double blocks. Thus, there are 150 possible subsets.
Fig. 82b
Here is one fairly satisfactory combination with a pair of solutions: pieces 1, 2, 3, 7, 8, and 12. Can the reader improve upon this? The Pin-Hole Puzzle and Corner Block Puzzle are not really burrs. They sneaked into this chapter as close relatives. This theme is carried forward in Chapter 13 and Chapter 22.
The number of practical ways that 24 notched sticks are symmetrically assemblable is very limited. Only one is known to the author, shown in Fig. 83. It uses 23 identical pieces and one key piece having an extra notch. With an illustration to follow, assembly of the puzzle is mostly a test of dexterity. There is also a surprising solution that uses 24 identical pieces without any key piece, and it requires even more dexterity.
Fig. 83
The really interesting feature of this puzzle set is that other interlocking assemblies are possible using fewer pieces, making it practically unique among burr puzzles. Two such solutions appear in Fig. 84. The one on the left is the standard six-piece burr, using five regular pieces and one key piece. Note the unusual symmetry of the one on the right, which uses nine regular pieces and one key piece. There is another neat solution, left for the reader to discover, that uses 16 regular pieces and has fourfold symmetry.
In order to be satisfactory, the pieces must be made accurately, with the length exactly three times the width. A version of this puzzle is produced by Pentangle under the name Squirrel Cage.
Fig. 84